Codeforces Round #285 (Div. 2)

はい。
リアルタイムの開催回に追いついてしまうと参加記との書き分けがどうするもんかと悩む。。
http://codeforces.com/contest/501

A. Contest

ざっくりと大意

・式がウチのブラウザで見ると点がかすれてて中黒にしか見えなかったんですが、

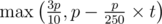
画像だけ抜き出してアップで見ると確かにカンマなので色々酷い。
・max(3p/10, p-p/250*t)で点数を出して勝ち負けや引分を判定すれば良い。

方針のようなもの

・max(3p/10, p-p/250*t)の式のとおりに判定する。

a,b,c,d=map(int,raw_input().split())

def judge(p,t):
    return max((3*p)/10, p-(p/250)*t)

print 'Misha' if judge(a,c)>judge(b,d) else 'Vasya' if judge(a,c)<judge(b,d) else 'Tie'

a,bは250で割り切れる数であることが保証されているのでint型のみで計算ができるようになっている。。。はず。。。

B. Misha and Changing Handles

ざっくりと大意

・名前変更のクエリが時系列順で並んでいるのを最後のクエリまで見て変更があった人の最初と最後の名前を出力する。

方針のようなもの

・クエリを追いかける。

n=int(raw_input())
old,new=[],[]
for i in xrange(n):
    a,b=map(str,raw_input().split())
    if a in new:
        new[new.index(a)]=b
    else:
        old.append(a)
        new.append(b)
print len(new)
for i in xrange(len(new)):
    print old[i],new[i]

解き直した時にちょっと連想配列を使おうかと思ってみたが処理途中でひたすらvalueの方にだけ処理が続きそうで意味がなさそうだったので配列2つで処理することにしました。クエリの変更前の名前が配列newになければ全く新しいクエリなので変更前の名前をoldに、変更後の名前をnewに入れる。配列newに変更前の名前がある人は既に過去に名前変更が発生している人なので配列newに入ってる前回の変更後で最新の名前=今回のクエリで変更前の名前を、今回のクエリで変更の最新の名前に入れ替える。クエリを全部処理し終わると配列のoldとnewで変更があった人の最初と最後が同じ番目に入ってるのでそれを出力する。

C. Misha and Forest

ざっくりと大意

・0からn-1で合計n個の頂点の森をなすグラフがある？？
・各頂点に対して直接接続された頂点の数とそれらの頂点番号のxorの値が与えられる？？
これがサンプルの1つ目の状態の図

n=3で頂点が0から2まである。 2 3 だと頂点0と接続されている頂点は1,2の2つあって、1と2のxorで3になる。
1 0 だと頂点1と接続されている頂点は0の1つあって、0のxorは0になる。
1 0 だと頂点2と接続されている頂点は0の1つあって、0のxorは0になる。

方針のようなもの

・そうだ、とりあえずパクろう。 mootalkさんのhttp://codeforces.com/contest/504/submission/9410339

n=int(raw_input())
xor,rem,q=[],[],[]
ed=0
for i in xrange(n):
    deg,s=map(int,raw_input().split())
    rem.append(deg)
    xor.append(s)
#辺の数を数えておく
    ed+=deg
#次数が1のものから処理するので入力時に次数が1のものは処理候補リストに入れておく
    if deg==1:
        q.append(i)
#グラフ全体の辺の数は入力で与えられた辺の総数を2で割れば良い
print ed/2

ind=0
lenq=len(q)
while ind<lenq:
    i=q[ind]
#次数が1のものはその時点で辺の先の頂点がxorリストに入っている値で確定するので出力
    if rem[i]==1:
        print i,xor[i]
#その辺の反対側?の頂点からxorの値を除く、辺の次数も1減らす
        xor[xor[i]]^=i
        rem[xor[i]]-=1
#辺の次数が1になったものは処理候補リストに入れる
        if rem[xor[i]]==1:
            q.append(xor[i])
            lenq+=1
    ind+=1

グラフが森の状態とは閉路がない,ループになる箇所がない,すべての頂点に1つ以上の辺があり他の頂点と接続されていることが保証されるっぽい。
この問題での処理では次数が1、辺が1つしか無いものは出力して取り除く？ので頂点がドコにも接続されていないものが発生するが辺を出力した後ならそれは問題ないっぽい。辺の数が少しずつ減っていく中で次数が1の頂点は尽きることがないっぽい。